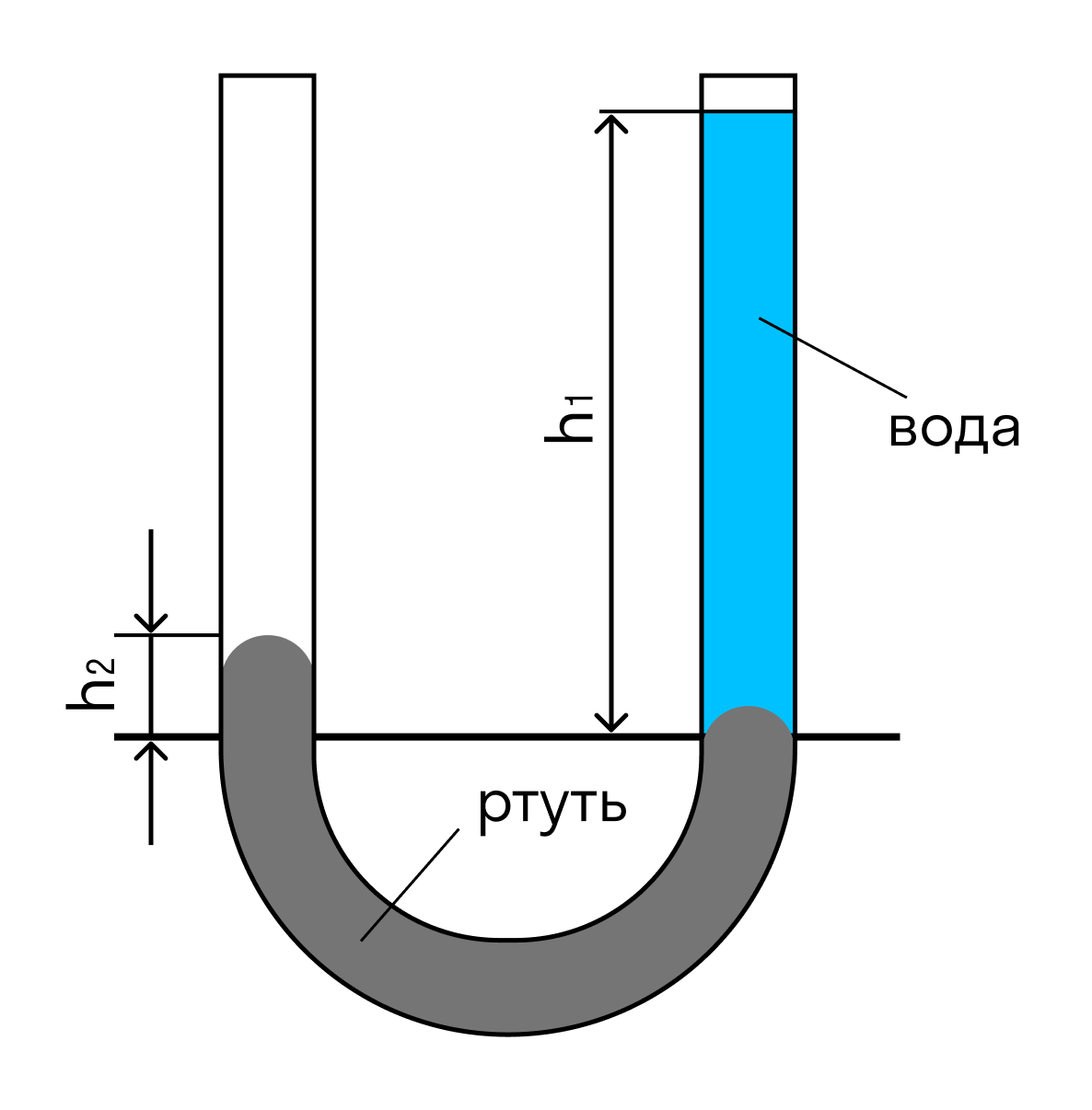
Способы определения высоты сосуда, наполненного водой

Физика изучает различные физические явления и их закономерности. Одно из таких явлений – агрегатные состояния вещества. Жидкости – это одно из состояний, в котором находится вода. Многие из нас знают, что высота столба жидкости в сосуде зависит от давления жидкости на дно сосуда. Но как рассчитать эту высоту?

В физике существует формула, которая позволяет решить эту задачу. Формула объема жидкости в сосуде выглядит следующим образом: объем жидкости равен площади поверхности сосуда, умноженной на высоту столба жидкости. Если мы знаем объем и высоту столба жидкости, то можем рассчитать площадь поверхности сосуда. Таким образом, мы можем найти высоту столба жидкости в сосуде, зная объем и размеры сосуда.

Для решения данной задачи необходимо использовать теорию давления жидкости. При наличии свободной поверхности жидкости, на нее действует атмосферное давление. Поэтому давление жидкости на дно сосуда состоит из давления атмосферного и давления столба жидкости. После применения формулы решения задачи, получаем значение давления жидкости на дно сосуда, которое равно величине давления атмосферного плюс давление столба жидкости.

Расчет давления жидкости на дно и стенки сосуда

При изучении задач, связанных с определением высоты жидкости в сосуде, важно также рассчитать давление, которое жидкость оказывает на дно и стенки сосуда. Это представляет интерес с точки зрения практического применения данной теории, например, при определении глубины водоема или объема жидкости в баке.

Расчет давления жидкости на дно и стенки сосуда осуществляется с использованием закона Паскаля. Согласно этому закону, давление, создаваемое жидкостью, передается во все направления равномерно. То есть, давление на дно и стенки сосуда будет одинаковым.

Формула для расчета давления жидкости на дно или стенки сосуда выглядит следующим образом:

P = ρgh

где:

• P — давление жидкости на дно или стенки сосуда, выраженное в паскалях (Па);
• ρ — плотность жидкости, выраженная в килограммах на кубический метр (кг/м³);
• g — ускорение свободного падения, примерное значение которого равно 9,81 м/с²;
• h — высота столба жидкости над точкой, для которой рассчитывается давление, выраженная в метрах (м).

Итак, чтобы найти давление на дно или стенки сосуда, мы знаем все величины в формуле, кроме высоты h. Решение задачи сводится к определению высоты столба жидкости над точкой.

Например, предположим, что у нас есть однородный сосуд с водой и вы хотите найти высоту столба воды над дным сосуда. Сначала нужно определить высоту одного водяного столба, используя формулу Паскаля. Затем задачу можно упростить до применения теории агрегатных состояний вещества, так как данной составляющей у нас нет.

Давление на дно и стенки сосуда можно также обнаружить с помощью замены воды на другую жидкость, например, бензин. В этом случае, для расчета высоты столба бензина, нужно использовать формулу Паскаля с учетом плотности бензина.

Зная высоту столба жидкости, мы можем легко расчитать давление на дно и стенки сосуда. Эта информация может быть полезной во многих практических задачах, и поможет вам лучше понять связь между глубиной жидкости и создаваемым давлением.

Содержание:

1. Определение высоты сосуда с помощью давления

• 1.1. Зависимость высоты жидкости от давления
• 1.2. Примеры задач на определение высоты сосуда
• 1.3. Формулы и решения для определения высоты сосуда

2. Определение высоты сосуда с использованием агрегатных состояний

• 2.1. Связь между давлением и высотой жидкости
• 2.2. Примеры задач на определение высоты сосуда с использованием агрегатных состояний
• 2.3. Формулы и решения для определения высоты сосуда с использованием агрегатных состояний

3. Сравнение различных способов определения высоты сосуда

• 3.1. Преимущества и недостатки использования давления
• 3.2. Преимущества и недостатки использования агрегатных состояний
• 3.3. Выбор наиболее подходящего метода определения высоты сосуда

Расчет давления жидкости на дно и стенки сосуда

Когда задача состоит в нахождении высоты жидкости в сосуде, можно использовать агрегатные состояния для решения этой задачи. Нам известна плотность жидкости, сила тяжести воды и площадь основания сосуда, которые сообщающиеся между собой через стенки сосуда будут давить на жидкость.

Для вычисления высоты жидкости воспользуемся формулой давления жидкости на дно и стенки сосуда:

P = ρgh

где P — давление жидкости на дно и стенки сосуда, ρ — плотность жидкости, g — ускорение свободного падения, h — высота жидкости.

Применение этой формулы позволяет найти высоту жидкости в сосуде, основываясь на её плотности и давлении. Затем можно использовать найденную высоту для решения других задач, например, для вычисления объёма жидкости.

В случае если сосуд имеет одну открытую сторону, например, через клапан, что является типичным примером для большого класса задач, возникает задача определения давления в сосуде.

Если жидкость сообщающимися сосудами находится на одной высоте, то давление в этих сосудах будет одинаковым. Эта особенность сообщающихся сосудов базируется на том, что жидкость не сопротивляется деформации и обладает свободной поверхностью.

Важно знать, что во время вычисления давления в сосуде используется площадь основания, а не объем жидкости.

Таким образом, в задачах на определение высоты жидкости в сосудах и на нахождение давления в сосуде применяется формула давления жидкости на дно и стенки сосуда, при условии равного давления на всю поверхность жидкости в сосудах, объем независим.

Примеры применения данной формулы включают расчет давления в жидкости, определение высоты в сосуде с жидкостью, а также решение задач по определению объема и глубины жидкости в сосудах.

Примеры применения и задача

Мы знаем, что жидкость имеет свойства, которые отличают ее от газов и твердых тел. Жидкость характеризуется тем, что она существует в состоянии, когда ее молекулы практически не меняют своего положения, но могут перемещаться относительно друг друга. Это состояние называется жидким.

Одним из важных свойств жидкости является давление. Оно зависит от глубины i поверхности жидкости, а также от ее плотности и составляющих ее молекул. Давление в жидкости равномерно распределяется по всей ее объему и сохраняется на всех уровнях.

Давление жидкости на дно сосуда можно вычислить с помощью формулы:

P = p * g * h

где P — сила давления (в паскалях), p — плотность жидкости (в кг/м^3), g — ускорение свободного падения (9.81 м/с^2), h — высота столба жидкости.

Зная высоту столба жидкости, мы можем вычислить давление, которое она оказывает на дно сосуда.

Например, если у нас есть сосуд с бензином, плотность которого равна 750 кг/м^3, и высота столба бензина в сосуде составляет 1 метр, мы можем использовать формулу для вычисления силы давления:

P = 750 * 9.81 * 1 = 7357.5 паскалей

Таким образом, давление бензина на дно сосуда составляет 7357.5 паскалей.

Знание этого расчета позволяет нам определить высоту сосуда с жидкостью, зная ее плотность и давление на дно сосуда. Этот пример является классическим примером применения формулы для вычисления высоты сосуда с водой.

Все эти задачи и примеры позволяют нам лучше понять и изучить свойства жидкостей, а также научиться решать задачи, связанные с ними.

Сообщающиеся сосуды

При использовании сообщающихся сосудов часто применяется закон Паскаля, согласно которому давление, создаваемое жидкостью, распространяется и сохраняется во всех направлениях равномерно. Это означает, что давление, создаваемое столбом жидкости в одном сосуде, будет одинаковым и в других связанных сосудах.

Решение задач на нахождение высоты столба жидкости в сообщающихся сосудах может быть рассчитано с использованием физических законов и формул. Одной из основных формул в данной тематике является формула давления в жидкости:

P = pgh

где P — давление, p — плотность жидкости, g — ускорение свободного падения, h — высота столба жидкости.

Например, если известно содержание воды в одном сосуде и площадь поперечного сечения второго сосуда, и требуется найти высоту столба воды во втором сосуде, можно использовать следующую формулу:

h = (P2 — P1) / (pg)

где h — искомая высота столба воды, P1 и P2 — давления воды в первом и втором сосудах соответственно, p — плотность воды, g — ускорение свободного падения.

Также, чтобы найти высоту столба жидкости, можно использовать формулу:

h = (P1 — P2) / (pg)

где h — искомая высота столба жидкости, P1 и P2 — давления жидкости в первом и втором сосудах соответственно, p — плотность жидкости, g — ускорение свободного падения.

Теория сообщающихся сосудов находится в курсе физики и используется для решения задач, например, определения высоты столба воды или глубине сосуда по объему и площади воды.

Одним из примеров применения сообщающихся сосудов является использование поршня и клапана. При открывании клапана между сосудами создается сообщающееся состояние, где давление жидкости будет одинаковым в обоих сосудах. Это позволяет использовать принцип равенства давлений для решения задачи.

Таким образом, понимание принципа работы сообщающихся сосудов и умение использовать соответствующие формулы помогает решать задачи, связанные с определением высоты столба жидкости в таких сосудах.

Жидкое агрегатное состояние

Одной из ключевых характеристик жидкости является ее плотность, которая зависит от массы данного объема жидкости. Для тех, кто думает, что плотность жидкости равна нулю, необходимо знать, что это не так. Масса жидкости равна произведению плотности на объем, и поэтому плотность всегда присутствует.

Одной из величин, с которой мы можем работать при расчете задач на определение высоты жидкости в сосуде, является давление, оказываемое жидкостью на дно этого сосуда. Для этого мы можем использовать уравнение Герона-Паскаля, которое связывает давление, площадь и силу, действующую на данную площадь.

Также, для расчета высоты жидкости в сосуде, мы можем использовать закон Архимеда, который гласит, что плавающее тело в жидкости испытывает силу, равную весу вытесненной жидкости. Эта сила зависит от плотности жидкости и объема вытесненной ею жидкости. При равенстве сил веса и силы Архимеда, плавающее тело полностью погружается в жидкость, а если сила веса больше силы Архимеда, то тело оказывается под водой, но еще частично выпирает из жидкости.

Таким образом, для определения высоты жидкости в сосуде можно использовать различные формулы и зависимости, которые основаны на законах теории жидкостей и газов.

Примеры задач, которые мы можем решать с помощью данных формул и законов, включают расчет высоты столба жидкости, находящейся в сообщающихся сосудах, или вычисление давления, оказываемого жидкостью на определенную площадь.

Важно знать, что при расчете высоты жидкости в сосуде необходимо учитывать множество факторов, таких как размеры сосуда, площадь его дна, плотность жидкости и другие параметры. Также при решении задач на определение высоты жидкости можно использовать принципы гидростатики и гидромеханики.

Для удобства решения задач на определение высоты жидкости в сосуде, мы также можем использовать разные инструменты, такие как клапаны и поршни, которые помогают управлять уровнем жидкости.

Применение сообщающихся сосудов

Одной из задач, решаемых с помощью сообщающихся сосудов, является нахождение высоты сосуда с водой. Для этого необходимо знать плотность воды (обычно принимается равной 1000 кг/м3) и уровень жидкости в сосуде. С помощью формулы давления в жидкости P = ρ * g * h, где P — давление, ρ — плотность жидкости, g — ускорение свободного падения, h — высота столба жидкости, можно вычислить высоту столба воды, если известна разность давлений на двух уровнях. Например, если на одном уровне давление равно 7 Паскалям, а на другом — 5 Паскалям, то разность давлений будет равна 2 Паскалям.

Сообщающиеся сосуды также позволяют вычислить объем вещества в сосуде. Для этого необходимо знать площадь поперечного сечения сосуда и высоту столба жидкости. С помощью формулы объема сосуда V = S * h, где V — объем сосуда, S — площадь поперечного сечения, h — высота столба жидкости, можно вычислить объем вещества, находящегося в сосуде.

Примеры применения сообщающихся сосудов можно найти в различных областях, например, в гидротехнике или химии. В гидротехнике используются сообщающиеся сосуды, чтобы определить уровень воды в реке или озере. В химии они применяются для проведения различных экспериментов, а также для контроля уровня вещества в реакторе или резервуаре.

Использование сообщающихся сосудов имеет свои выигрыши и ограничения. Сообщающиеся сосуды позволяют быстро и точно определить высоту столба жидкости или газа, а также объем вещества в сосуде. Однако, они действуют только в условиях сохранения состояния агрегатного состояния вещества и величины плотности. Если изменится агрегатное состояние вещества или плотность, то результаты расчета могут быть неправильными.

Преимущества	Ограничения
— Быстрое и точное определение высоты столба жидкости или газа	— Действуют только в условиях сохранения агрегатного состояния и плотности
— Возможность определения объема вещества в сосуде

Таким образом, использование сообщающихся сосудов позволяет решать различные задачи, связанные с определением высоты столба жидкости или газа, а также объема вещества в сосуде. Однако, для получения точных результатов необходимо учитывать ограничения и условия эксперимента.

Давление столба жидкости

Давление, оказываемое столбом жидкости на его дно, можно определить с помощью формулы:

P = pgh

где P — давление столба жидкости, p — плотность жидкости, g — ускорение свободного падения, h — высота столба жидкости.

Таким образом, зная плотность жидкости и высоту столба, можно вычислить давление на дно сосуда. Скажем, в случае, если дно сосуда имеет площадь S, можно также вычислить силу, оказываемую столбом жидкости на дно, используя следующую формулу:

F = P * S

Это позволяет рассчитать, например, давление столба жидкости на дно большого судна или шлюза.

Кроме того, давление столба жидкости может изменяться в зависимости от состояния жидкости. В агрегатных состояниях, таких как жидкое или газообразное, межмолекулярные силы играют роль в формировании давления. Например, при использовании клапана на поверхности воды, можно создать давление на брусок или поршень, открывающийся под действием силы веса столба воды.

Также нам может быть известна площадь поверхности, которую жидкость покрывает в сосуде. В этом случае мы можем использовать формулу:

P = F / S

где P — давление на поверхности, F — сила, оказываемая столбом жидкости на поверхность, S — площадь поверхности.

Зная плотность жидкости и давление на поверхности, мы также можем использовать эту формулу для расчета высоты столба жидкости.

Таким образом, давление столба жидкости играет важную роль во многих задачах физики и науки. Его использование позволяет определить высоту столба жидкости в сосудах и решить различные задачи, связанные с жидкостями.

Как найти высоту сосуда с водой

Для решения задач, связанных с определением высоты сосуда с водой, необходимо учитывать принципы гидростатики и использовать формулы, связанные с давлением.

Если дано, что уровень жидкости в двух сосудах, сообщающихся между собой, находится в состоянии равновесия, то можно применить принцип Архимеда и формулу давления на глубине.

Формула давления на глубине определяется как произведение плотности жидкости, ускорения свободного падения и глубины:

давление = плотность * ускорение свободного падения * глубина

Если известны площади поверхности сосудов и высота столба жидкости в одном из них, то можно использовать соотношение оказываемых сил на площади. При этом предполагается, что жидкость находится в агрегатном состоянии и не образует паров.

Например, если у нас есть два сосуда, сообщающиеся между собой, и в одном из них находится жидкость, а в другом — только воздух, то давление на дно каждого сосуда будет одинаковое.

Однако, если в одном из сосудов находится мелко залитая жидкость, а в другом — жидкое состояние на глубине, то давление на дно будет разным.

Примеры задач на нахождение высоты сосуда с водой могут быть следующими:

1. Сосуд имеет площадь поверхности 0,5 м², а высота столба воды в нем составляет 7 м. Найти давление на дно сосуда.
2. Есть два сосуда, сообщающиеся между собой, с площадями их поверхностей 1 м² и 2 м². Уровень жидкости в сосудах находится в состоянии равновесия. Найти высоту столба жидкости в первом сосуде, если во втором сосуде он составляет 5 м.

Таким образом, зная площадь поверхности сосуда, состояние жидкости и давление, можно определить высоту столба воды.

Видео:

Гидростатический парадокс

Гидростатический парадокс by GetAClass — Физика в опытах и экспериментах 430,314 views 9 years ago 5 minutes, 25 seconds