Методы решения задач по воде для учащихся 5 класса

На уроке по математике в 5 классе проходит увлекательный урок на тему «Задачи по воде». В этом уроке ученики узнают, как решать различные задачи, связанные с движением объектов в воде. Данный урок поможет им развить навыки аналитического мышления, логики и применения математических знаний на практике.

Один из примеров задач, которые решают на этом уроке, звучит так: «Лодка проплыла по озеру до впадения в реку за 4 часа. Вниз по течению реки она против течения в течение 3 часов. Найдите скорость течения реки, если скорость лодки в стоячей воде равна 6 км/ч». Для решения этой задачи необходимо вычислить разности времени, за которое лодка преодолевает каждую часть пути. Затем можно записать уравнение и определить значение неизвестной, которое и будет ответом.

Другая задача, которую обычно рассматривают на этом уроке, звучит так: «В течение 4 часов против течения реки лодка преодолела 24 км. Вверх по течению реки в течение 5 часов лодка преодолела 35 км. Найдите скорость течения реки и скорость лодки в стоячей воде». Для решения этой задачи нужно составить две системы уравнений и решить их методом подстановки или методом вычисления обратного времени.

В ходе урока ученики также узнают о движении объектов в воде, о различных типах лодок: гребные, моторные, плоты, катера и теплоходы. Они научатся определять скорость течения реки, скорость лодки в стоячей воде и скорость движения лодки по отношению к берегу. Ученикам понадобится записать все данные задачи и составить уравнение для ее решения.

Урок проходит в интерактивной форме с использованием слайдов. Ученикам предлагается решить несколько задач по воде, записать свои действия и подписи к рисункам, а затем устно объяснить свои действия и полученные результаты. Это поможет им лучше понять и запомнить материал, а также развить навыки самостоятельного решения задач.

Задачи на движение по реке

Уроки математики и обучения на практике

В классе можно решать задачи по движению по реке на уроке математики. Ученики смогут применить свои знания и навыки для решения практических задач. Решение таких задач позволяет применить собственную логику и алгебру для нахождения ответа.

Ответы на задачи по движению по реке полезны для учащихся, чтобы они могли лучше понять взаимосвязь между движением лодок, реки и скоростей. Узнать, как скорость реки влияет на скорость движения лодки, можно с помощью решения этих задач.

Пример задачи

Рассмотрим пример задачи на движение по реке: теплоход движется впадает в реку и стоит на месте. Одновременно с тем в противоположном направлении плывет моторная лодка. За 5 часов теплоход проплыл 60км, против течения реки. За то же время лодка проплыла 120км по реке. Найдите скорость туриста в стоячей воде и скорость течения реки.

Решение: Пусть скорость теплохода в стоячей воде равна v1, а скорость течения реки равна v2.

Теплоход движется против течения реки, поэтому его скорость равна разности скоростей теплохода и течения реки:

v = v1 — v2

За время 5 часов теплоход проплыл 60км, значит его скорость равна:

v × 5 = 60

Отсюда находим скорость теплохода:

v1 — v2 × 5 = 60

Аналогично, лодка движется по течению реки, поэтому её скорость равна сумме скоростей лодки и течения реки:

v = v1 + v2

За время 5 часов лодка проплыла 120км, значит её скорость равна:

v × 5 = 120

Отсюда находим скорость лодки:

v1 + v2 × 5 = 120

Теперь имеем систему уравнений:

v1 — v2 × 5 = 60

v1 + v2 × 5 = 120

Решаем эту систему уравнений и находим значения скорости туриста в стоячей воде и скорости течения реки.

5 класс Решение задач на движение по воде презентация к уроку по алгебре 5 класс

Класс задач

В данной презентации рассматриваются задачи на движение по воде, в которых объекты по различным причинам движутся на реке или в воде.

Решение задач

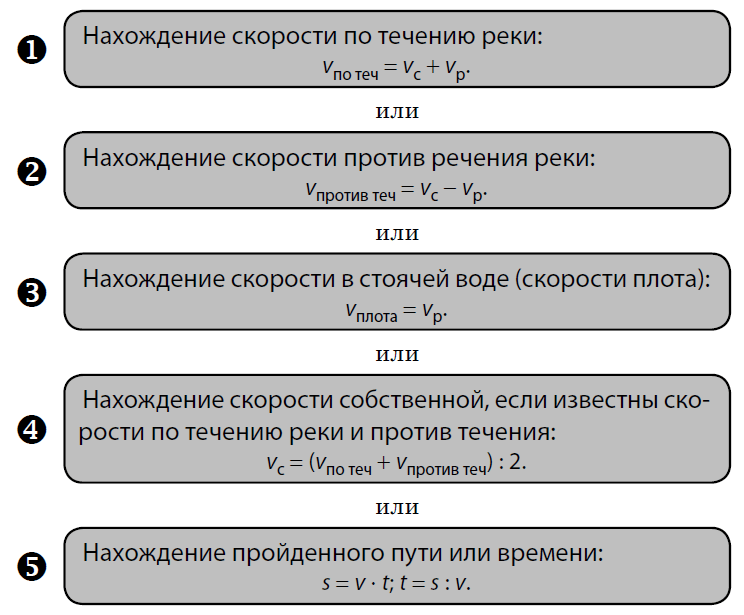
Прежде чем приступить к решению задач на движение по воде, необходимо уяснить следующие понятия и формулы.

Решение задач на движение по воде включает в себя следующие шаги:

1. Определить данные, представленные в задаче.
2. Выделить из данной информации необходимые для решения задачи данные.
3. Определить известные и неизвестные величины.
4. Составить уравнение или систему уравнений, используя данные о скорости и времени движения объекта по воде.
5. Решить уравнение или систему уравнений для определения неизвестных величин.
6. Проверить полученный ответ.

Пример задачи на движение по воде

Два катера одновременно отправились из двух противоположных причалов к друг другу. Один катер двигался со скоростью 15 км/ч в сторону течения реки, а второй катер – со скоростью 20 км/ч против течения реки. Путь между причалами составляет 75 км. Найдите время, которое требуется катерам для встречи. Течение воды в реке равно 5 км/ч.

Решение:

Для решения данной задачи, необходимо использовать формулу для нахождения времени движения:

v = s / t

Для первого катера:

Скорость первого катера в стоячей воде составляет 15 км/ч. Учитывая скорость течения воды (5 км/ч), скорость первого катера относительно берега составляет 10 км/ч. Для движения против течения реки скорость первого катера будет равна разности скорости движения катера и скорости течения реки:

vпервого катера = 15 — 5 = 10 км/ч

Для второго катера:

Скорость второго катера в стоячей воде составляет 20 км/ч. Учитывая скорость течения воды (5 км/ч), скорость второго катера относительно берега составляет 25 км/ч. Для движения по течению реки скорость второго катера будет равна сумме скорости движения катера и скорости течения реки:

vвторого катера = 20 + 5 = 25 км/ч

Общее время, которое потратят катера на встречу, определяется по формуле:

t = s / vтотальная

Для движения отдельного катера:

tпервого катера = 75 / 10 = 7.5 часа

tвторого катера = 75 / 25 = 3 часа

Обратите внимание, что каждый из катеров преодолевает половину пути, прежде чем встретиться с другим катером.

Ответ: Встреча катеров произойдет через 3 часа и 30 минут после того, как каждый из них отправился из причалов.

Скачать

В данной теме рассмотрим задачу о движении туристов на воде. Два туриста на лодке проплыли через озеро. Одного из них движение не затратило времени, так как он двигался по течению реки. Второй турист двигался против течения, поэтому потратил на этот путь определенное время.

Сначала решим задачу в устной форме, затем перейдем к вычислениям.

Устное решение задачи

Пусть моторная скорость туристов, движущихся вниз по реке, равна Vтечения, а их собственная скорость равна Vсобственная. Найдем разность этих скоростей: Vтечения — Vсобственная = Vихода. Зная время движения туристов, можно определить путь, который они преодолели.

Если лодка движется вверх по течению реки, то путь, который пройдет лодка, определяется собственной скоростью движения туриста. Заметим, что в этом случае лодка не сможет самостоятельно вернуться к причалу, так как ей понадобится время, чтобы преодолеть собственную скорость течения.

Вычисление решения задачи

Допустим, туристы проплыли через озеро за 2 часа, при этом первый турист двигался по течению реки, а второй против течения. Для простоты будем считать, что моторная скорость течения равна 5 км/ч, а скорость движения туристов в стоячей воде равна 3 км/ч.

Поэтому разность скоростей будет равна: Vтечения — Vсобственная = 5 — 3 = 2 км/ч.

Зная, что лодка двигалась вверх по течению в течение 2 часов, можно вычислить путь, который турист преодолел: 2 часа * 2 км/ч = 4 км.

Таким образом, если турист потратил 2 часа на движение вверх по течению, то он пройдет путь длиной 4 км.

Данный пример позволяет понять, как решать задачи по воде, используя математику. Ознакомьтесь с другими задачами и презентацией к уроку, чтобы узнать больше о теме.

Видео:

Задачи на движение по воде. Виды скоростей. Как решать задачи по математике в 5 классе. Часть 17.

Задачи на движение по воде. Виды скоростей. Как решать задачи по математике в 5 классе. Часть 17. de Математика от Баканчиковой 5 746 vues il y a 1 an 17 minutes