- Описание трубопровода с переменным сечением для транспортировки воды.
- Задача 3-9
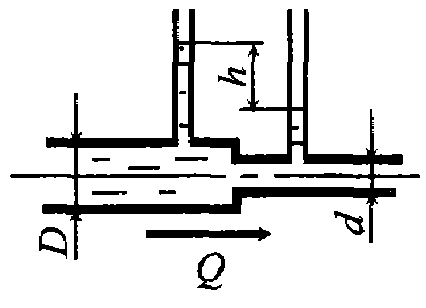
- Примеры решения задач Пример № 71 Определить расход жидкости Q в горизонтальном трубопроводе диаметром d1 = 0.2 м имеющем сужение диаметром d2 = 0.12 м (рис)
- Видео:
- Эффект Вентури и трубка Пито (видео 16) | Жидкости | Физика
Описание трубопровода с переменным сечением для транспортировки воды.
Трубопроводы с переменным сечением – это важная часть инфраструктуры современного мира. Они широко применяются для транспортировки различных жидкостей, включая воду, нефть и другие.
В данной статье мы рассмотрим примеры задач, связанных с расчетами скорости и напорной энергии в трубопроводах переменного сечения. Для определения этих величин нам понадобятся уравнения Бернулли и пьезометров.
Рассмотрим, например, задачу о горизонтальном трубопроводе с переменным сечением. Пусть диаметром на участке 1-2 равен d1, а на участке 2-3 – d2. В каждом сечении определено значение скорости жидкости: v1 на участке 1-2 и v2 на участке 2-3. Задача заключается в том, чтобы определить скорость жидкости по всей длине трубопровода, а также расход потока.
Для решения этой задачи используем уравнение Бернулли, которое описывает движение жидкости в трубопроводе. Согласно уравнению Бернулли, сумма скоростей, давлений и потерь энергии в любом сечении трубопровода равна константе. Также, мы используем пьезометрическую линию для определения напорной энергии и потерь давления в жидкости на разных участках трубопровода.
Задача 3-9
Рассмотрим задачу о течении жидкости по трубопроводу переменного сечения, через который протекает вода. Чтобы решить эту задачу, мы сначала принимаем уравнение Бернулли, которое учитывает движение жидкости на различных сечениях.
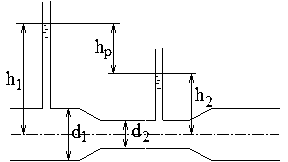
Для примера возьмем горизонтальный трубопровод № 012 с диаметром D1 = 0,2 м, по которому перемещается ламинарный поток воды. Нам нужно определить пьезометрическую (гидростатическую) скорость жидкости, если на рисунке видно сужение трубопровода с диаметром D2 = 0,1 м.
Задача состоит в определении скорости движения жидкости и потерь давления между двумя сечениями в трубопроводе. Для решения мы определяем уравнение Бернулли, которое учитывает потери энергии.
Рис. 1: Сечения трубопровода
| Сечение | Диаметром |
|---|---|
| Сечение 1 | D1 = 0,2 м |
| Сечение 2 | D2 = 0,1 м |
Используя уравнение Бернулли и учитывая различные режимы движения жидкости в трубопроводе (ламинарный, турбулентный), мы можем определить скорости и потери давления в системе. Также необходимо принять во внимание пьезометры, которые показывают давление жидкости на каждом сечении.
Итак, для решения задачи мы будем использовать следующие уравнения:
| № | Уравнение |
|---|---|
| 1 | Разницей пьезометров |
| 2 | Уравнение Бернулли |
Решая уравнения с учетом заданных значений диаметров и пьезометрической скорости, мы получим ответ на задачу.
Примеры решения задач Пример № 71 Определить расход жидкости Q в горизонтальном трубопроводе диаметром d1 = 0.2 м имеющем сужение диаметром d2 = 0.12 м (рис)
Дана задача о расходе жидкости в трубопроводе переменного сечения. Для решения данного примера воспользуемся уравнением Бернулли.
Получим уравнение для определения расхода используя пьезометрическую линию.
| Участок | Параметры |
|---|---|
| 1 | диаметр d1 = 0.2 м |
| 2 | диаметр d2 = 0.12 м |
Рассмотрим режимы движения жидкости в трубопроводе:
- Если жидкость движется с ламинарной скоростью, то режим называется ламинарным.
- Если жидкость движется с турбулентной скоростью, то режим называется турбулентным.
Для определения расхода Q воспользуемся уравнением Бернулли для двух сечений (1 и 2) трубопровода:
$$\frac {p_1}{
ho}+\frac {V_1^2}{2}+g \cdot h_1=\frac {p_2}{
ho}+\frac {V_2^2}{2}+g \cdot h_2$$
Где:
- $$p_1$$ и $$p_2$$ — давление на участках 1 и 2 соответственно;
- $$
ho$$ — плотность жидкости; - $$V_1$$ и $$V_2$$ — скорости потока на участках 1 и 2 соответственно;
- $$g$$ — ускорение свободного падения;
- $$h_1$$ и $$h_2$$ — напорные высоты на участках 1 и 2 соответственно.
Для ламинарного потока в трубопроводе с постоянным диаметром скорость V и расход Q связаны следующим соотношением:
$$Q=\frac {\pi \cdot d^2}{4} \cdot V$$
где $$d$$ — диаметр трубопровода.
В нашем примере задачи, имеем следующие данные:
- Диаметр трубопровода d1 = 0.2 м;
- Диаметр сужения d2 = 0.12 м.
Используя уравнение Бернулли, можем выразить давления на участках 1 и 2:
$$p_1=\frac {1}{2} \cdot
ho \cdot V_1^2$$
$$p_2=\frac {1}{2} \cdot
ho \cdot V_2^2$$
Обозначим скоростями V1 и V2 скорости потока на участках 1 и 2 соответственно. Для ламинарного потока действуют следующие соотношения:
$$V_1=\frac {Q}{\frac {\pi \cdot d_1^2}{4}}$$
$$V_2=\frac {Q}{\frac {\pi \cdot d_2^2}{4}}$$
Подставим данные в уравнение Бернулли:
$$\frac {\frac {1}{2} \cdot
ho \cdot V_1^2}{
ho}+\frac {Q^2}{2 \cdot \left(\frac {\pi \cdot d_1^2}{4}
ight)^2}+g \cdot h_1=\frac {\frac {1}{2} \cdot
ho \cdot V_2^2}{
ho}+\frac {Q^2}{2 \cdot \left(\frac {\pi \cdot d_2^2}{4}
ight)^2}+g \cdot h_2$$
Упростим уравнение, используя соотношения для расхода Q:
$$\frac {\frac {1}{2} \cdot
ho \cdot V_1^2}{
ho}+\frac {Q^2}{2 \cdot \left(\frac {\pi \cdot d_1^2}{4}
ight)^2}+g \cdot h_1=\frac {\frac {1}{2} \cdot
ho \cdot V_2^2}{
ho}+\frac {Q^2}{2 \cdot \left(\frac {\pi \cdot d_2^2}{4}
ight)^2}+g \cdot h_2$$
$$\frac {Q^2}{\left(\frac {\pi \cdot d_1^2}{4}
ight)^2}+\frac {Q^2}{\left(\frac {\pi \cdot d_2^2}{4}
ight)^2}=\frac {2 \cdot g \cdot (h_2-h_1)}{
ho}$$
$$Q^2 \left( \frac {1}{\left(\frac {\pi \cdot d_1^2}{4}
ight)^2} + \frac {1}{\left(\frac {\pi \cdot d_2^2}{4}
ight)^2}
ight) = \frac {2 \cdot g \cdot (h_2-h_1)}{
ho}$$
$$Q = \sqrt{\frac {2 \cdot g \cdot (h_2-h_1)}{
ho} \cdot \left( \frac {\left(\frac {\pi \cdot d_1^2}{4}
ight)^2}{\left( \frac {\pi \cdot d_1^2}{4}
ight)^2 + \left( \frac {\pi \cdot d_2^2}{4}
ight)^2}
ight)}$$
Теперь, подставив известные значения в полученную формулу, можем определить расход жидкости в трубопроводе с заданными сечениями:
$$Q = \sqrt{\frac {2 \cdot 9.8 \cdot (h_2-h_1)}{1000} \cdot \left( \frac {\left( \frac {\pi \cdot 0.2^2}{4}
ight)^2}{\left( \frac {\pi \cdot 0.2^2}{4}
ight)^2 + \left( \frac {\pi \cdot 0.12^2}{4}
ight)^2}
ight)}$$
Таким образом, расход жидкости Q в горизонтальном трубопроводе с диаметром d1 = 0.2 м и сужением диаметром d2 = 0.12 м будет равен полученному значению.
Видео:
Эффект Вентури и трубка Пито (видео 16) | Жидкости | Физика
Эффект Вентури и трубка Пито (видео 16) | Жидкости | Физика by KhanAcademyRussian 673,200 views 4 years ago 8 minutes, 53 seconds