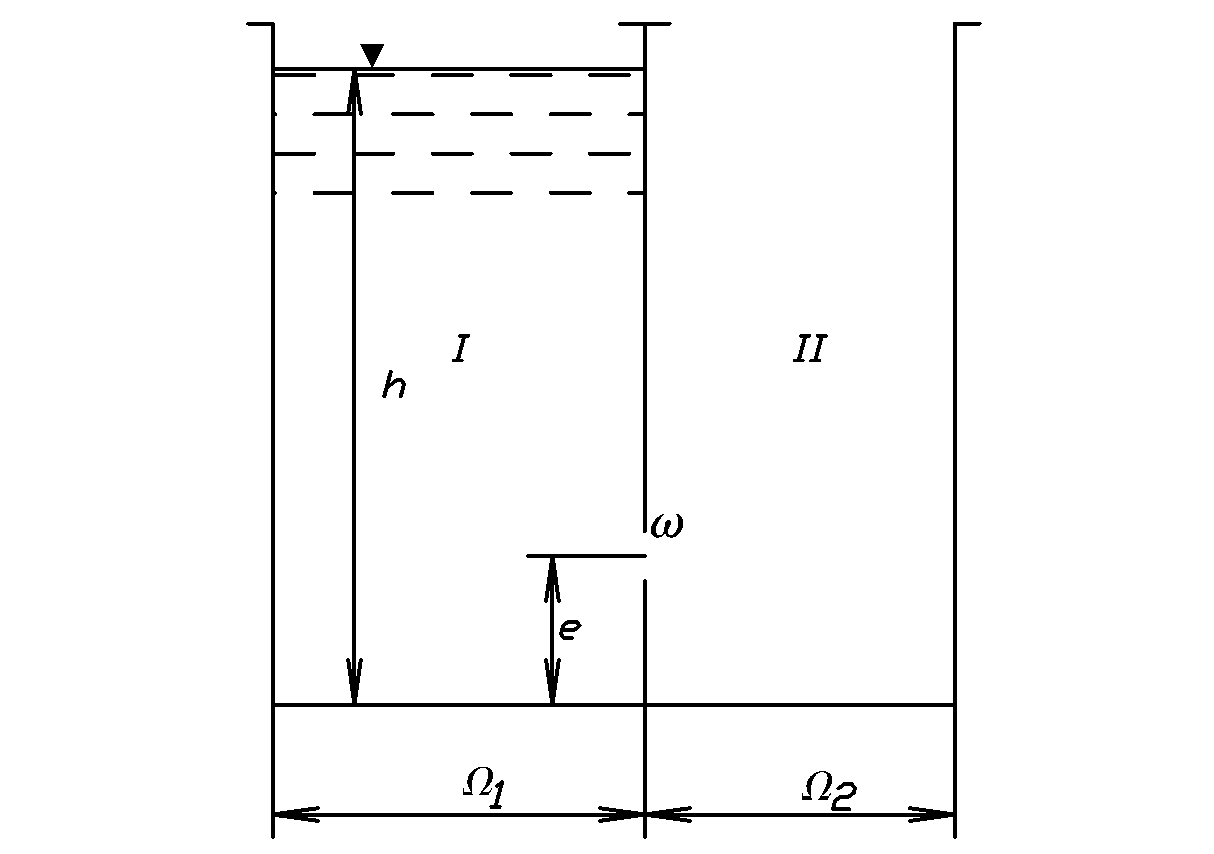
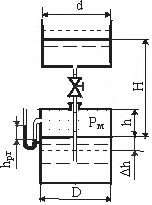
Как решить задачу с водой в резервуаре?

В 2015 году появилась первая, и можно сказать, идиотская задача про резервуар с водой. Суть ее такая: есть два резервуара, один объемом в 13 литров, а второй — неадекватные 2015 литров, из которого через некоторое время начинают наполнять первый резервуар. Задача заключается в том, чтобы вычислить время, через которое первый резервуар будет заполнен полностью, если из второго резервуара может вытекать 9 литров в час, а в первый течет 3 литра в минуту.

Давайте решим задачу пошагово. В первую очередь определим основные данные: объем первого резервуара составляет 13 литров, а объем второго — 2015 литров. Кроме того, из второго резервуара вытекает 9 литров в час, а в первый поступает 3 литра в минуту. Пропускная способность трубы между резервуарами равна 3 литрам в минуту.

Для решения задачи воспользуемся уравнением «объем = производительность x время». Мы знаем, что объем первого резервуара составляет 13 литров, а второй резервуар заполняет первый. Пусть x — это время, через которое первый резервуар будет полностью заполнен. Тогда уравнение будет иметь вид: 13 = 3x. Преобразуя его, получим x = 13/3 минуты или около 4 минуты и 20 секунд.

Итак, ответ на задачу: первый резервуар будет наполняться полностью за примерно 4 минуты и 20 секунд. При этом второй резервуар будет постепенно терять объем, так как его вода перетекает в первый резервуар. Эта задача показывает, какая смешанная задача получается, когда вода поступает одновременно из двух источников и устойчивое состояние достигается путем смешивания двух жидкостей.

Задача про резервуар с водой

Мы хотим найти скорость наполнения резервуара горячей водой, то есть сколько литров в минуту бассейна заполняет горячей водой.

Запишем уравнение первой задачи. Обозначим через В_труба объём воды, наполняемой через первую трубу в минуту, в л.

Время заполнения резервуара через первую трубу:

Время = объём резервуара / общая производительность = 2015 л / (13 л/мин) = 155 мин

Из условия задачи мы знаем, что время заполнения резервуара через вторую трубу составляет 20 минут. Найдём производительность второй трубы.

Объём резервуара = объём горячей воды + объём холодной воды.

Объём холодной воды = производительность второй трубы * время = В_труба * 20 мин.

Таким образом, производительность второй трубы равна: 2015 л — В_труба * 20 мин / 20 мин = 2015 л — В_труба.

Из условия задачи также следует, что объём холодной воды, втекающей через вторую трубу, равен производительности второй трубы, умноженной на время: 4 л/сек * 20 мин = 4800 л.

Теперь приравняем объём холодной воды, втекающей через вторую трубу:

Объём холодной воды = производительность второй трубы * время = (2015 л — В_труба) * 20 мин.

Решим получившееся уравнение:

4800 л = (2015 л — В_труба) * 20 мин.

4800 л = 2015 л * 20 мин — В_труба * 20 мин.

4800 л — 2015 л * 20 мин = -В_труба * 20 мин.

-В_труба * 20 мин = -4800 л + 2015 л * 20 мин.

В_труба * 20 мин = 4800 л — 2015 л * 20 мин.

В_труба = (4800 л — 2015 л * 20 мин) / 20 мин.

В_труба = 4800 л / 20 мин — 2015 л.

В_труба = 240 л/мин — 2015 л.

Таким образом, скорость наполнения резервуара горячей водой составляет 240 литров в минуту при условии, что через вторую трубу пропускается 2015 литров воды.

Задача нахождения скорости заполнения резервуара горячей водой решена. Мы вычислили, что горячая вода заполняет бассейн со скоростью 240 л/мин, при этом через вторую трубу пропускается 2015 л/мин воды.

Решение текстовой задачи В13 2015 Задача на трубы

В данной задаче рассматривается резервуар с водой, который наполняется с помощью нескольких труб. Задача заключается в определении времени, за которое резервуар будет заполнен до определенного уровня.

Задача довольно идиотская, поскольку уравнение, которое описывает заполнение резервуара, очень сложное.

В условии задачи даны следующие данные:

• Пропускная способность каждой трубы — скорость наполнения резервуара через одну трубу в литрах в минуту;
• Объем резервуара — сколько литров нужно заполнить;
• Какая часть резервуара уже заполнена.

Задача решается путем составления и решения уравнения.

Сначала находим скорость наполнения резервуара всеми трубами вместе. Для этого суммируем производительность каждой трубы.

Тогда уравнение заполнения резервуара выглядит следующим образом:

Объем резервуара = (скорость наполнения резервуара всеми трубами вместе) * (время)

Таким образом, в задаче В13 на трубы нужно найти время, за которое резервуар будет заполнен до указанного уровня, при известной производительности каждой трубы и объеме резервуара.

Очень важно обратить внимание на единицы измерения: скорость производительности трубы задана в литрах в минуту, а объем резервуара — в литрах. Поэтому в уравнении необходимо использовать одинаковые единицы измерения.

Решение задачи на трубы заключается в вычислении времени, которое потребуется для заполнения резервуара до указанного уровня.

Иногда в задачах дана информация о скорости наполнения резервуара через одну трубу и скорости расхода резервуара через другую. В этом случае задача решается путем составления и решения системы уравнений.

Таким образом, задача В13 2015 на трубы сводится к решению уравнений и вычислениям. В условии задачи даны все необходимые данные, поэтому решение задачи возможно.

Видео:

Текстовая задача из реального варианта ЕГЭ 2021. про трубы, у каждой свой резервуар

Текстовая задача из реального варианта ЕГЭ 2021. про трубы, у каждой свой резервуар автор: Репетитор по математике Инна Леонидовна 49 переглядів 5 місяців тому 6 хвилин і 3 секунди